<< Click to Display Table of Contents >> Navigation:  Impeller > Mean line design > Blade properties > Blade angles > Outlet triangle > Calculation details

 

Circumferential component of blade congruent flow can be calculated as follows:

.

The slip coefficient is a function of blade angle, number of blades and the meridional geometry (see e.g. GÜLICH/WIESNER etc.):

.

The relation of the blade angle to the velocity components is:

 .

A swirl has to be produced by the impeller in accordance to the design specific work (here without pre-swirl) with the Euler equation:

.

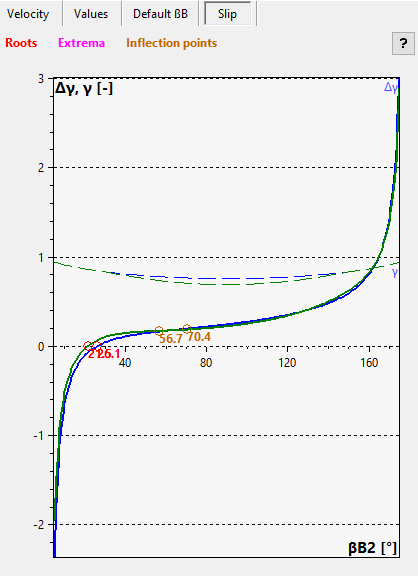
These equations build a set that cannot be solved explicitly but numerically. To this an equation representing the difference of the slip coefficient according to the definition and according to the particular model can be used:

 .

One can test this equation with different values of β2B and will get a function of the form Δγ = f(β2B). This function together with γ = f(β2B) according to the definition of slip coefficient is displayed for hub and shroud. Also, points of interest apart from zero are illustrated such as minimum and maximum and inflection. The equation is fulfilled at zero.